Relato: Distância entre dois pontos no plano

Autor: Edivaldo Gomes de Ávila
Instituição: Colégio Estadual Prof. João Farias da Costa
Município: Nova Cantu - Pr
Conteúdo: Distância entre dois pontos no plano
Série: 3º Ensino Médio

---

Este material foi elaborado como requisito de avaliação final da oficina Geogebra, sob orientação da docente, assessora pedagógica Giselli Mocelin Martins, da equipe da Coordenação Regional de Tecnologia na Educação do Núcleo Regional de Educação, de Campo Mourão.

Justificativa

A resolução gráfica de uma atividade proposta em sala de aula e desenvolvida algebricamente nem sempre dá ao aluno uma noção mais ampla da situação problema que se quer resolver ou ainda fica preso as fórmulas matemáticas muitas vezes sem sentido algum, se não para o momento de abstração que o leva a um resultado sem sentido.

Levar ao conhecimento do aluno a disponibilidade de uma ferramenta de construção gráfica que encontrasse ao seu alcance no laboratório de informática da escola e propiciar sua utilização pode trazer ao aluno a visualização real da situação e encher de ilustração e sentido a resolução algébrica que é mais abstrata.

Aprendendo a utilizar o GeoGebra na verificação gráfica de exercícios desenvolvidos algebricamente em sala de aula, pode também aproximar o aluno, estreitando seu interesse pela matemática e com isso a valorização do laboratório de informática como ferramenta de prática e experimentação e não somente como biblioteca virtual como muitas vezes se encontra.

Objetivos

• Calcular e representar graficamente distâncias entre 2 pontos no gráfico cartesiano.
• Obter as coordenadas do ponto P equidistante aos pontos A e B.
• Verificar se correto os cálculos algébricos antes desenvolvidos e se têm de fato sentido o resultado obtido.

Desenvolvimento metodológico

Uma vez que o professor em sala de aula tenha superado os pré-requisitos teóricos que o conteúdo exige, propõe-se que os alunos desenvolvam a atividade proposta. A resolução algébrica da atividade deve ser bem explorada tentando deixar o mínimo de dúvidas possível quanto ao objetivo que se quer alcançar.

Alcançando-se o resultado da atividade por todos os participantes, o professor deverá propor em seguida uma ilustração gráfica da atividade, que deverá ser desenvolvido com o auxilio do professor e a utilização de folhas quadriculadas para facilitar a construção da atividade sem muita perca de tempo.

A exploração visual e a aferição com régua das medidas das distâncias entre os pontos obtidos na construção gráfica alcançada pelos alunos, deverá ser feita por todos os participantes com o questionamento do professor sobre coordenadas e distâncias equidistantes que deverá direcionar e promover um melhor entendimento.

Num terceiro momento, é interessante que o professor antes de tudo leve os alunos ao laboratório de informática e apresente aos participantes o software GeoGebra. Uma aula deverá ser o suficiente para que os alunos se familiarizem com as ferramentas que o GeoGebra oferece, lembrando que se já houve esse momento em outra oportunidade, este passo não será necessário.

Após o professor ter apresentado, já no laboratório de informática, uma breve revisão da atividade que será desenvolvida, segue a orientação para a construção da atividade como proposta no passo a passo.

Observação Algébrica e Geométrica durante a construção deverão ser abordadas e comparadas com a atividade já realizada em sala.

Recursos

• Na construção geométrica em sala de aula, estará disponível papel quadriculado, compassos e réguas para construção e aferição.
• Laboratório de Informática, Software GeoGebra e material já produzido em sala de aula.

Avaliação

O sucesso da atividade com avaliação positiva no seu desenvolvimento será obtida se o participante:

• Compreende e relaciona as propriedades geométricas aplicadas;
• Observa com entendimento a aplicabilidade do cálculo da distância entre 2 pontos no plano;
• Participa até o final da atividade demonstrando interesse em relação à matemática o conteúdo e o seu desenvolvimento no laboratório de informática.

Referências

PARANSecretaria de estado da Educação. Diretrizes Curriculares da Educação básica. Matemática. Curitiba, Seed, 2008.
SILVA, Claudio Xavier da. FILHO, Benigno Barreto. Matemática Aula por Aula. 2. ed. São Paulo: FTD, 2005.

Atividade de Verificação Gráfica

Determine as coordenadas do ponto P, sabendo que ele pertence ao eixo das abscissas e é equidistante aos pontos A(2,3) e B(-2,0).

Passo a passo da atividade

Parte 1

1. Abra o software (programa) Geogebra.
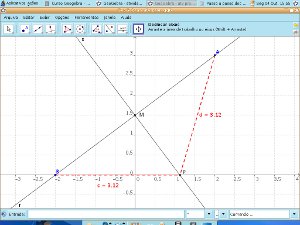
2. insira os pontos A(2,3) e B(-2,0). No campo de entrada digite: A=(2,3) e Enter. No campo de entrada digite: B=(-2,0).
3. Insira o ponto P que pertence ao eixo das abscissas. No campo de entrada digite: P=Ponto [EixoX].
4. Faça os segmentos AP e BP (B3). Mude sua propriedade para pontilhado, espessura 5 e cor vermelha.
5. Meça os segmentos AP e BP (B7).
6. Com a ferramenta mover (B1), mova o ponto “P” de modo a obter a mesma distância entre os segmentos AP e BP. Verifique na janela de Álgebra as medidas dos segmentos.

• É possível definir as coordenadas do ponto P equidistante aos pontos A e B?
• O que acontece?
• Qual a coordenada do ponto P?

Parte2

1. Abra um arquivo novo.
2. Insira os pontos A(2,3) e B(-2,0). No campo de entrada digite: A=(2,3) e Enter. No campo de entrada digite: B=(-2,0) e Enter. Observe os pontos e suas coordenadas na janela de álgebra.
3. Insira uma reta (B3) que passa pelos pontos A e B. Renomeie para reta r, clicando com o botão direito sobre a reta, renomear. Na janela de álgebra, sobre a equação geral da reta, clicando com o botão direito do mouse selecione Equação y=kx+d.
4. Obtenha o ponto médio do segmento AB (B2). Renomeie o ponto para M. (Na janela de álgebra, com o botão direito do mouse ou no menu editar propriedades, básico, nome).
5. Construa um reta perpendicular (B4) ao segmento AB que passa pelo ponto M. (Selecionando a ferramenta e clicando sobre a reta e o ponto M). Renomeie a reta para s. Na janela de álgebra mude a equação da reta para y=kx+d. Compare as duas equações.
6. Obtenha o ponto de intersecção entre a reta s e o eixo das abscissas x (B2). Renomeie o ponto para P.
7. Faça os segmentos AP e BP (B3). Mude sua propriedade para pontilhado, espessura 5 e cor vermelha.
8. Meça as distâncias entre os pontos A e P e os pontos B e P (B7).Questionamentos

• Qual é a distância entre os pontos A e P e o ponto B e P?
• O ponto P é Solução para o questionamento inicial?
• O que podemos observar na janela de álgebra em relação as duas equações das retas? (Coeficiente Angular e Condição de Perpendicularismo).
• Observe a janela de álgebra, o que há de comum entre as duas equações das retas e as coordenadas do ponto M? O que esse valor representa nas equações?
• Em comparação a construção em sala de aula com papel quadriculado e régua, esta facilita em algo?
• Os conceitos utilizados na parte 1 desta atividade em relação aos conceitos utilizados na parte 2, quais dificuldades e/ou facilidades podemos observar?
• O GeoGebra pode nos auxiliar no estudo da geometria analítica, entre outros conteúdos matemáticos?